2. 北京大学 空间信息集成与3S工程应用北京市重点实验室, 北京 100871
2. Beijing Key Lab of Spatial Information Integration and 3S Application, Peking University, Beijing 100871, P. R. China
传统的传感器模型以共线方程为理论基础,建立这类严格的传感器模型,需获取各种成像参数[1](对航空影像而言包括内方位元素和外方位元素初值,对卫星影像而言包括轨道参数和传感器平台的方位参数及焦距等)。近年来,航空影像和无人机影像得到了广泛应用[2],其中无人机影像的使用又对影像的正射拼接等应用提出了较高要求。然而此类非航天遥感影像在获取过程中,平台的不稳定性导致了影像间的相对位置不确定度增大,且重叠度不一,造成了经典的基于共线方程的光束法平差方法不能满足影像解算要求。
例如IKONOS等线阵推扫式遥感影像,它的特点是长焦距和窄视场角,这是由其高空间分辨率的特点决定的。对于这种成像几何关系,如果采用基于共线方程的物理传感器模型描述,将导致定向参数之间的强相关性,从而影响定向的精度和稳定性。但多数厂家会额外提供一种通用的传感器模型,即有理函数模型(RFM)。作为一种通用的广义传感器模型,在航天影像解算中可替代基于严格共线方程的几何模型。如Tao等[3]针对摄影测量过程,对有理函数模型进行了深入剖析,首先提出了有理函数模型参数的最小二乘迭代解法;Grodecki等[4]则对基于有理多项式系数的高分辨率影像进行了区域网平差,并对其结果进行了分析和评价;其他的研究大多聚焦在RFM模型在航天影像中的立体定位算法[5, 6]或将正则化方法应用到算法中[7],并给出了补偿RFM模型系统误差的物方方案和像方方案[8-10]。利用RFM可以解决航天传感器的定标问题[11],还可将其用于几何定位[12], 并在一定程度上替代SAR成像模型[13]和基于视差角的极坐标方法[14-16]。
由于RFM可以直接回避成像的几何过程,直接建立起像点和空间坐标之间的关系,由此可以应用于无人机等影像获取平台不稳定的多类传感器中。近来关于RFM与严格共线方程之间的转换问题也引起了大家的重视[17],但整体来讲RFM在航空以及近景遥感领域研究较少,故本文对RFM在非航天遥感影像中的解算进行了探索。首先通过增加正则化的最小二乘方法对RFM进行求解,然后利用航空遥感影像数据证明RFM的通用性,为RFM在无人机等近景遥感影像的推广提供理论支持。
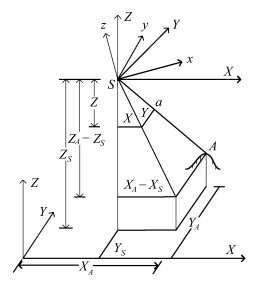
1 空中三角测量基础-共线方程共线条件以中心投影构像为数学基础,是各种摄影测量处理方法的重要理论基础,例如单像空间后方交会、双像空间前方交会以及光束法区域网平差等问题的原理,都是基于共线条件。其基本思想是:首先建立像空间坐标系、地面摄影测量坐标以及像空间辅助坐标系。依据中心投影成像原理中S、a及A三点共线条件,将地面点A发出的投影光线SA在像平面上的构像a点表示为像空间坐标系及像空间辅助坐标系中的坐标,并将地面点A表示成为地面摄影测量坐标系及像空间辅助坐标系中的坐标,利用点a及A的像空间辅助坐标之间的几何关系,从而建立像点a在像空间坐标系与地面点A在地面坐标系中坐标之间的几何关系。如图 1所示。
|
图 1 相机中心、像点与地面点的共线关系示意图 Fig.1 Collinear relationship diagram of camera center, image point and the corresponding ground point |
其理论表达形式如下式:
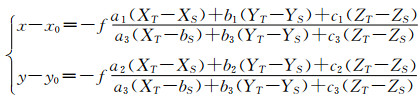
|
(1) |
式中, (x, y, -f)为像点a在像空间坐标系中的坐标;(X, Y, Z)为像点a在像空间辅助坐标系中的坐标;(XT, YT, ZT)为地面点A在地面摄影测量坐标系中的坐标;(XS, YS, ZS)为投影中心S的地面摄影测量坐标;(XA-XS, YA-YS, ZA-ZS)为地面点A在像空间辅助坐标系的坐标。
在共线方程优化过程中应用最多的为光束法平差,即以一张像片组成的一束光线作为一个平差单元,以中心投影的共线方程作为平差的基础方程,通过各光线束在空间的旋转和平移,使模型之间的公共光线实现最佳交会,将整体区域最佳地纳入到控制点坐标系中,从而确定加密点的地面坐标及像片的外方位元素。
2 有理函数模型 2.1 RFM定义有理函数模型(rational function model,RFM)中,将像点坐标(r, c)表达为相应地面点空间坐标(X, Y, Z)为自变量的多项式的比值。为增强参数求解的稳定性, 将地面坐标和影像坐标归一化到-1和1之间,目的是减少计算过程中由于数据数量级差别过大引入的舍入误差。对一幅影像,定义如下比值多项式:
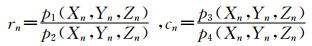
|
(2) |
式中,rn、cn分别为像素的行列数;(Xn, Yn, Zn)是对应目标点的地面坐标。各正则化参数由式(3)得到:
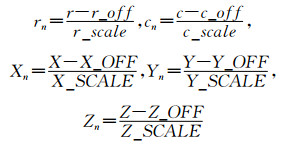
|
(3) |
式中,r_off和c_off为影像像素坐标的偏移值,r_scale和c_scale为影像像素坐标的比例值;同样地,X_OFF,Y_OFF和Z_OFF是地面坐标的偏移值,X_SCALE, Y_SCALE和Z_SCALE是地面坐标的比例值。
多项式中每一项的各个坐标分量X、Y以及Z的幂最大不超过3, 每一项各个坐标分量幂的总和也不超过3(通常取1, 2, 3)。另外,分母项p2和p4的取值可以有两种情况: p2=p4(可以是一个多项式, 也可以是常量1),p2≠p4。每个多项式的形式为:
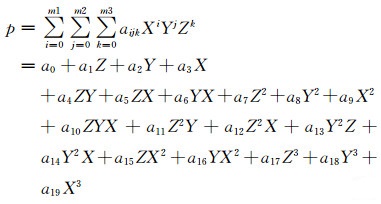
|
(4) |
式中,aijk是多项式的系数(两个多项式分母中的常数项恒为1)。(2)式也可写成下列形式:
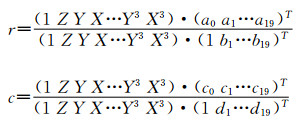
|
(5) |
多项式的系数称为有理多项式系数(rational polynomial coefficient,RPC)。在模型中由光学投影引起的畸变表示为一阶多项式,而地球曲率、大气折射、镜头畸变等的改正,可由二阶多项式趋近,高阶部分的其它未知畸变可由三阶多项式模拟。(2)式是RFM的正解形式,其反解形式为:
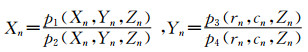
|
(6) |
RFM实质上是多项式模型的扩展,也是很多传感器模型的共同形式。
2.2 RFM的求解方案有理函数模型在解求系数过程时,根据情况不同,可以分为多种解求形式。例如多项式不同的阶数或分母相同与否都直接影响到所需的最少控制点个数。具体的结合形式见表 1。
| 表 1 RFM模型的9种情况 Table 1 Nine cases of rational function model |
表 1给出了9种情况下待求解RFM模型参数的形式、参数个数和需要的最少控制点个数。当RFM模型分母相同且恒为1时,退化为一般的三维多项式模型,模型分母相同但不恒为1,且在一阶多项式情况下,RFM模型退化为直接线性变换(direct linear transformation, DLT),而DLT是经典摄影测量中常用的几何模型,由此也看出RFM是一种广义的成像几何模型。
2.2.1 最小二乘方法解算RFM为了解算有理多项式系数RFM,并采用最小二乘原理优化结果,需要对(5)式进行线性化处理得出误差方程。线性化过程如下:
首先,由式(5)得到误差方程(7):
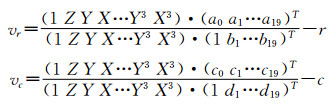
|
(7) |
令:
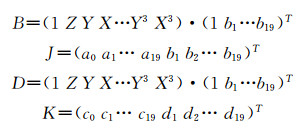
|
在式(7)中将r和c写成如下形式:
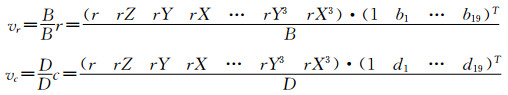
|
(8) |
代入(7)式得误差方程(9):
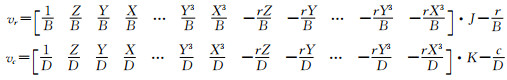
|
(9) |
或者是方程(10):
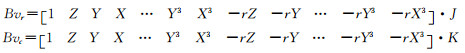
|
(10) |
式(9)和式(10)就是解算有理函数系数的误差方程式。只要有足够的控制点且分布均匀,就可以按上两式解算系数。足够个数的地面点数n(由于系数个数为78,所以n的个数不能小于39)的误差方程形式如式(11),为简便起见,只按(9)式中的第一式列出误差方程,其它情况与此类似:

|
(11) |
写成矩阵形式如下:
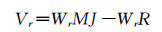
|
(12) |
式中, 
Wr可以看作是残差权矩阵,从而可以得法方程:
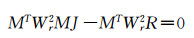
|
(13) |
由于原始误差方程式含有未知参数bi的函数B,所以是非线性的,故最小二乘的答解需要迭代进行。具体的作法为:首先取Wr为单位阵,可以解算出J的初值:J0=(MTM)-1MTR,作为所求参数的初值;在以后的第i次答解时,用前一次得到的参数Ji-1构造残差权矩阵Wr, 然后按(13)式答解未知参数Ji。迭代结束需要满足的条件是:
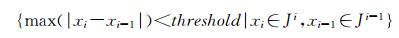
|
(14) |
通过法方程迭代直至满足上述条件,最终得到结果(多项式的系数)。
以上均是对像点坐标r列出误差方程求解的过程,以下讨论是将像点r和c联合求解的实用方程式。列方向求解过程与行方向求解过程类似,行列同时答解误差方程:
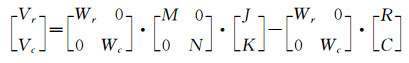
|
(15) |
矩阵表示为:
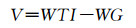
|
(16) |
法方程表示为:
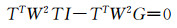
|
(17) |
同样地,先将W残差权矩阵置为单位阵,求解出I的初值,然后利用前一次求出的I值对所有参数赋值,按照(17)式迭代求解各参数值。(16)与(17)式分别是常用的有理函数模型误差方程式与法方程式。
有理函数模型的RFM可以在物理传感器模型各参数已知的情况下或者传感器模型参数未知的情况下求解,对应的解决方法是“与地形有关”(terrain-dependent)和“与地形无关”(terrain-independent)这两类方案。如果物理传感器模型已知,即严密成像几何模型已知的情况下,采用与地形无关的求解方式;否则,采用与地形有关的求解方式,这种解决方法的结果将会高度依赖于所输入的地表控制点精度与分布。
2.2.2 与地形无关的RFM求解方案如果有严格的传感器模型, 可以用该模型建立一组3维的目标格网点作为控制点来解算RFC。这些格网点的坐标可以利用严格的传感器模型来计算(通常是利用像坐标和高程值计算地面坐标的平面位置,其中高程值的确定是通过估计地面的起伏,在地面的起伏范围内取若干高程面),而不需要实际的地形信息, 因此这种解算方案与实际的地形无关。该方法的解算步骤为:
1) 影像空间格网点的选取;
2) 地面3维格网点的解算;
3) RFM系数的解算:用上述的层状控制点格网来解算RFM的系数;
4) 精度检查。
在无法获得地面详细信息时,可以利用上述方法来求解每幅影像的有理多项式系数,并且也为有理函数模型拟合精度的估计提供了一种方法。有理多项式系数可以用来进行图像正射校正或者用于立体定位(像对中每一幅影像的RFM均需要求出)。有理函数模型的这种特性非常重要,因为一些商业遥感影像提供商将物理传感器模型信息设为保密内容,但是用户们依然可以利用RFM对图像加以处理和利用。
2.2.3 与地形有关的求解方案在不能获得严格传感器模型参数时,就没有办法建立空间格网点。为了解算有理多项式系数,需要在地图或者DEM上测量获取像点、地面控制点与地面检查点的坐标。这种情况下,解法高度取决于实际的地形起伏、地面控制点的数量以及控制点的整体分布,很明显这种方法“与地形有关”。当传感器模型过于复杂很难建立或者对精度要求不高时,常采用这种方法来建立传感器模型。
2.3 TIKHONOV正则化正则化是指在求解不适定问题时,用一组与原不适定问题相“邻近”的适定问题的解去逼近原问题的解,这种方法称为正则化。不适定问题通常是病态的,并且不论是简单地还是复杂地改变问题本身的形式,都不会显著地改善病态问题。另一方面,病态问题不一定是不适定问题,因为通过改变问题的形式往往可以改善病态问题。
为了解决病态问题,一般采用Tikhonov正则化方法。Tikhonov正则化方法原理是在最小二乘准则的基础上,加入参数向量范数最小的条件,得到正则化解,对于Ax=y问题,Tikhonov正则化形式如下:
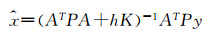
|
(18) |
式中,P为观测残差权矩阵,当K=E(单位矩阵)时,则Tikhonov正则化就变为有偏估计,这是一种考虑系统误差的方法。从线性代数的分析可知,矩阵的条件数总是大于或等于1。
在对有理多项式系数求解的过程中,由于地面点选取的不均匀性,容易导致矩阵TTW2T的条件数变大,最终使得迭代不收敛。为了改善矩阵TTW2T的条件数,在法方程中加入单位矩阵与一个微小量的乘积项。由于TTW2T矩阵通常是对称矩阵并且是半正定的,所以TTW2T+h2E项的特征值的范围是: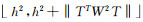
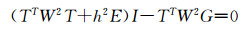
|
(19) |
由于正则化参数h的值决定了正则化结果,所以确定h的数值也是一项重要的工作。为确定h的数值,Tao等[3]在3阶RFM情况下,利用60个地面控制点和249个检查点及与其相应的像点坐标做了不同的实验,最终发现当h在[0.0002,0.008]范围内时,解求法方程的迭代次数少于6,且当h在该范围内时RFM结果较稳定。
3 实验与讨论 3.1 数据本实验所使用的材料是DMC(digital mapping camera)相机航空影像产品56张,影像大小为7680像素*13824像素。摄影仪焦距120 μm,航向重叠度:63.92%,旁向重叠度:30.39%。图 2为实验场景图。

|
图 2 利用RFM进行实验解算的DMC航空影像图 Fig.2 DMC aerial images used for RFM computation |
本研究从项目区域中选取了加密点成果作为后期解算RFM模型的原始数据,列于表 2。
| 表 2 控制点坐标(共70个加密点,这里仅列举15个加密点) Table 2 Coordinates of ground control points (15 out of 70 points are listed below) |
当获得空三加密点数据后,就可以对有理函数模型进行参数求解。本文根据已有控制点与检查点数据,采用了3阶带分母的有理多项式模型,利用了Tikhonov正则化方法对误差方程进行了正则化,在“与地形有关”的求解方案中解求出了有理多项式系数(RFM)。
由第2节内容得到像点坐标的误差法方程式为式(20):
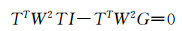
|
(20) |
经过Tikhonov正则化后的法方程形式表达如下:
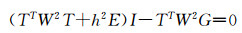
|
(21) |
当h取0.001时能够获得较理想的迭代次数与理想的精度。此时就可以利用最小二乘方法迭代求解RFM:

|
(22) |
式中,W(s)=W(I(s)), v(s)=G-TI(s)。具体的迭代方法为:首先取W为单位阵,可以解算出I的初值:I0=(MTM)-1MTG,作为所求参数的初值;在以后的第i次答解时,用前一次得到的参数I(s-1)构造残差权矩阵W,然后按(22)式答解未知参数I(s);迭代结束需要满足的条件是:
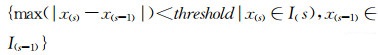
|
(23) |
通过法方程迭代直至满足上述条件,最终得到结果(多项式的系数)。
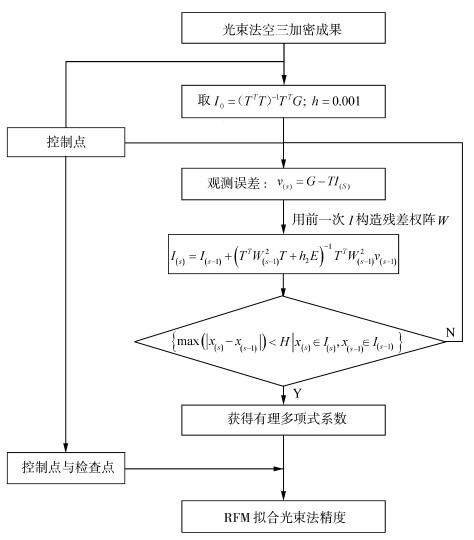
有理函数模型程序设计流程如图 3所示。
|
图 3 RFM解算航空遥感影像设计流程图 Fig.3 Flow chart of RFM solving aerial images |
对于单张影像,利用摄影测量商业软件ImageStation生成的加密点坐标分为地面控制点(55个)与地面检查点(15个)。对控制点、检查点及对应像点坐标归一化后得到归一化坐标。表 3所示为地面控制点和对应像点归一化坐标,表 4为检查点归一化坐标。
| 表 3 地面控制点及对应像点归一化坐标 Table 3 Regularized coordinates of ground control points and its corresponding image points |
| 表 4 地面检查点归一化坐标 Table 4 Regularized coordinates of ground check points |
用求解的RFM模型参数来计算控制点与检查点所对应的影像坐标,然后通过由严密成像几何模型所解算的控制点与检查点对应的影像坐标的差值,评定求解RFM模型参数的像方精度,表 5所示为最终由RFM解算航空遥感影像所得误差表。
| 表 5 影像坐标解算前后的差值 Table 5 Difference of images coordinates after solution |
由正解RFM模型解算出的控制点与检查点所对应的像点坐标和已有像点坐标之间的差值比较发现,仅有少数像点的误差在0.3(pixel)与0.5(pixel)之间,个别像点误差达到0.7(pixel)到0.9(pixel),大多数像点坐标差值均小于0.1。
实验验证过程中,RFM拟合精度随所选地面控制点的分布有较大的变化。本研究是在较多实验中所选取的一种比较理想的结果(见表 6),拟合精度平均为0.3(pixel),说明RFM拟合基于共线方程的光束法模型达到了比较高的精度。
| 表 6 基于RFM模型解算的航空遥感影像像方精度 Table 6 Image coordinates accuracy of aerial images using RFM solution |
此外,图 4所示为利用求得的RFM参数对所有实验影像进行解算得到的点云图像。通过房屋的边界以及道路的曲直程度可以看出RFM对航空影像的解算是能够满足专业生产要求的,这也从另一侧面反映出它在航空或无人机图像优化处理过程中的适用性。

|
图 4 利用RFM参数解算出的区域点云图像 Fig.4 Regional point clouds calculated by RFM parameters |
本文利用“与地形有关”的RFM求解方案对RFM拟合光束法模型的成果进行了展示,实现了基于正解的RFM的空中三角测量加密方法。此外,利用航空遥感数据实验验证了RFM模型的通用性,为无人机影像处理提供理论与实验依据。由于RFM不包含传感器的有关信息,能够实现传感器参数的有效隐藏,因此作为一种广义的传感器模型,有理函数模型在很大程度上可代替基于共线方程的光束法,用于非航天遥感影像的空三加密、立体重构以及正射校正等传统摄影测量工艺。
| [1] |
张剑清, 潘励, 王树根.
摄影测量学[M]. 武汉: 武汉大学出版社, 2009: 26-30.
Zhao J Q, Pan L, Wang S G. Photogrammetry[M]. Wuhan: Wuhan University Press, 2009: 26-30. |
| [2] |
郑鸿云, 赵红颖, 魏云鹏, 辛甜甜. 小型无人机快速最优化稳像方法研究[J]. 影像科学与光化学, 2016, 34(1): 51–58.
Zheng H Y, Zhao H Y, Wei Y P, Xin T T. The research of the small UAV optimal video stabilization[J]. Imaging Science and Photochemistry, 2016, 34(1): 51–58. DOI:10.7517/j.issn.1674-0475.2016.01.051 |
| [3] | Tao C V, Hu Y. A comprehensive study of the rational function model for photogrammetric processing[J]. Photogrammetric Engineering & Remote Sensing, 2001, 67(12): 1347–1357. |
| [4] | Grodecki J, Dial G. Block adjustment of high-resolution satellite images described by rational polynomials[J]. Photogrammetric Engineering & Remote Sensing, 2003, 69(1): 59–68. |
| [5] |
巩丹超, 邓雪清, 张云彬. 新型遥感卫星传感器几何模型——有理函数模型[J]. 海洋测绘, 2003, 23(1): 31–33.
Gong D C, Deng X Q, Zhang Y B. The geometric model of the new type sensor of remote sensing satellite-the rational function model[J]. Hydrographic Surveying and Charting, 2003, 23(1): 31–33. |
| [6] |
王鹏生, 贺少帅, 刘排英. 改化的有理函数模型在卫星影像定位中的应用[J]. 地理空间信息, 2017, 15(1): 74–76.
Wang P S, He S S, Liu P Y. The application of modified rational function model in satellite image location[J]. Geospatial Information, 2017, 15(1): 74–76. |
| [7] | Neumaier A. Solving ill-conditioned and singular linear systems:a tutorial on regularization[J]. Siam Review, 1998, 40(3): 636–666. DOI:10.1137/S0036144597321909 |
| [8] |
巩丹超, 张永生. 有理函数模型的解算与应用[J]. 测绘学院学报, 2003, 20(1): 39–42.
Gong D C, Zhang Y S. The solving and application of rational function model[J]. Journal of Institute of Surveying and Mapping, 2003, 20(1): 39–42. |
| [9] | Fraser C S, Hanley H B. Bias-compensated RFMs for sensor orientation of high-resolution satellite imagery[J]. Photogrammetric Engineering and Remote Sensing, 2005, 71(8): 909–915. DOI:10.14358/PERS.71.8.909 |
| [10] | Hartley R I, Saxena T. The cubic rational polynomial ca-mera model[C]. Image Understanding Workshop, 1997. 649-653. |
| [11] | Wang T Y, Zhang G, Jiang Y H, Wang S Y, Huang W C, Li L T. Combined calibration method based on rational function model for the Chinese GF-1 wide-field-of-view imagery[J]. Photogrammetric Engineering and Remote Sensing, 2016, 82(4): 291–298. DOI:10.14358/PERS.82.4.291 |
| [12] |
吴亚文, 鲁铁定. 利用有理函数模型的几何定位仿射变换方法[J]. 测绘科学, 2015, 40(4): 48–52.
Wu Y W, Lu T D. A affine transformation method of geometric positioning based on RFMS[J]. Science of Sur-veying and Mapping, 2015, 40(4): 48–52. |
| [13] |
张过, 费文波, 李贞. 用RFM替代星载SAR严密成像几何模型的试验与分析[J]. 测绘学报, 2010, 39(3): 264–270.
Zhang G, Fei W B, Li Z. Analysis and test of the substitutability of the RPC model for the rigorous sensor model of spaceborne SAR imagery[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(3): 264–270. |
| [14] | Zhao L, Huang S D, Yan L, Dissanayake G. A new feature parametrization for monocular SLAM using line features[J]. Robotica, 2015, 33(3): 513–536. DOI:10.1017/S026357471400040X |
| [15] | Yan L, Chen R, Sun H B, Sun Y B, Liu L, Wang Q. A novel bundle adjustment method with additional ground control points constraint[J]. Remote Sensing Letters, 2017, 8(1): 68–77. DOI:10.1080/2150704X.2016.1235809 |
| [16] | Sun Y B, Zhao L, Zhou G Q, Yan L. Absolute orientation based on distance kernel functions[J]. Remote Sensing, 2016, 8(3): 21. |
| [17] | Liu S J, Tong X H. Transformation between rational function model and rigorous sensor model for high resolution satellite imagery[C]. The International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, 2008. 3-11. |




